When we talk about teaching fractions in first grade, we're not starting with numerators and denominators. We’re starting with something far more intuitive: fair shares. It's all about making math real and building a gut-level understanding of what it means to have 'parts of a whole.' This playful, hands-on approach is what lays a powerful foundation for all future math success.
Why Early Fraction Concepts Matter in First Grade
Let's be honest—the word "fractions" can make even seasoned teachers a little nervous. For years, I felt like introducing them in first grade was just too much, too soon. My whole perspective changed when I stopped thinking "this is advanced math" and started thinking "this is just about sharing."
That simple shift in mindset was a game-changer in my classroom. Fractions were no longer scary symbols on a page. Instead, they were about splitting a cookie with a friend, dividing crayons into equal groups, or making sure everyone got the same amount of Play-Doh. Every six-year-old intuitively gets that.
Building a Foundation to Prevent Fraction Phobia
When we introduce fractions through play and real-world scenarios, we do something incredibly powerful: we stop "fraction phobia" before it even starts. We’re creating positive, successful first experiences with a topic that can become a massive stumbling block later on.
This early exposure isn't just about feel-good moments; it has a huge academic impact. The achievement gap in fraction knowledge is a well-documented problem. In one startling finding, 50% of U.S. eighth graders couldn't correctly order three simple fractions. This tells us the initial understanding built in the early grades isn't solid enough. You can explore more about these findings on early fraction comprehension.
By focusing on the foundational ideas of partitioning and equal shares in first grade, we are directly addressing this gap before it even begins to widen. It's preventative teaching at its best.
Connecting Fractions to the Bigger Picture
The concepts we cover in a first-grade fractions unit aren't just isolated skills—they're the bedrock for so many future math ideas. Think about it:
- Division: Understanding how to split a whole into equal parts is the very definition of division.
- Ratios and Proportions: The idea that a fraction represents a relationship between a part and a whole is essential for understanding ratios.
- Measurement: Concepts like half an inch or a quarter of a cup rely on a solid understanding of fractions.
- Telling Time: Phrases like "half past" and "quarter to" are directly linked to fractional parts of an hour.
Teaching fractions in first grade is like planting seeds that will grow throughout a child's entire math journey. The time we put in now pays off for years, making it one of the most rewarding parts of the curriculum. And when you're planning these crucial lessons, tools like Kuraplan can be a huge help, generating visuals and activities that make concepts like 'equal parts' clear and engaging for young learners.
Building Understanding with Concrete Fraction Activities

Before we even think about picking up a pencil, our first graders need to get their hands on fractions. This is the concrete stage, and it’s where real, sticky learning begins. We're taking an abstract idea and making it tangible, playable, and honestly, unforgettable.
Think of it this way: you're turning a tricky math concept into a game of fairness, something every six-year-old understands instinctively. It’s less about rules and more about making sure everyone gets an equal piece of the pie—or in this case, the Play-Doh cookie!
Start with What They Know: Food and Fun
Food is the universal language of first grade, making it the perfect starting point for fractions. You don’t need a bunch of fancy manipulatives; everyday items from the kitchen or art cart work wonders.
Fraction Pizzas: Give each student a paper plate “pizza.” Have them fold it right down the middle to make two equal shares. This is the perfect moment to introduce the word halves. Then, fold it again to make four equal pieces and introduce fourths. Let them decorate each part before they "share" their creation.
Play-Doh Cookies: Roll out some Play-Doh “cookies” and hand out plastic knives. The challenge? Cut a cookie in half to share with a friend. Ask them, "Are the pieces fair? Are they equal?" This simple act of cutting reinforces the core idea of equal parts.
Sharing Snacks: Even snack time is a teachable moment. Got a long pretzel rod? Ask a student how they could break it in half to share. This brings the vocabulary right into their world, making it stick.
These simple activities build a foundation you can’t get from a worksheet. Students are physically making the fractions, connecting the action of dividing with the concept of equal parts. That muscle memory is what they'll rely on later.
From the Playroom to the Classroom
Look beyond food—the toys already in your classroom are secretly powerful fraction tools. Everyday building blocks and art supplies can be repurposed for some seriously good math learning, tapping right into their natural instinct to play.
When you're gathering materials, you might even think about how Montessori materials for home turn abstract ideas into hands-on experiences. You can apply the same principles with what you already have.
Teacher Tip: The most important word at this stage is "equal." I'm constantly asking, "Are the parts equal?" or "Is this a fair share?" That repetition helps them internalize that fractions aren't just any old pieces, but equal pieces of a whole.
LEGO bricks, for instance, are fantastic for this. A long 8-stud brick can be the whole. Then you can show how two 4-stud bricks are the halves that click together to make that whole. It's a perfect visual.
Structuring Your Hands-On Lessons
To keep the learning focused, it really helps to have a clear sequence for your hands-on activities. I always introduce one concept at a time—start with the "whole," then move to halves, and only then introduce fourths. Don't rush it. Mastery here is all about deep, physical understanding.
Here’s a simple progression I like to follow:
- Introduce the "Whole": Spend a whole session just identifying the "whole" object before you divide it. This is the whole pizza, the whole cookie, or the whole building block.
- Explore Halves: Dedicate a full lesson or two just to making halves. Use lots of different materials to show that a half is always one of two equal pieces.
- Introduce Fourths/Quarters: Once they've got halves down, bring in fourths by showing them how to split a whole into four equal parts. Have them compare the size of a fourth to a half.
Finding the right activities and pacing is key to building a solid foundation in fractions for first grade. If you're looking to save some planning time, a resource like Kuraplan's basic fractions plan for first graders has ready-to-go activities that fit perfectly with this hands-on approach.
By spending plenty of time on these concrete experiences, you're doing more than just teaching a math unit. You’re building confident, flexible thinkers who see fractions not as something scary, but as a natural part of the world all around them.
Connecting Hands-On Learning to Visual Models

After all the fun with Play-Doh and paper pizzas, it's time to help our students translate that physical experience onto paper. This is the crucial bridge from the concrete to the visual—moving from doing to representing.
This step is where their hands-on discoveries about fractions for first grade start to look like the math they’ll see in books. We're not jumping straight into abstract worksheets. Instead, we're guiding them to draw what they just did. If they split a cookie in half, the very next step is drawing a circle and showing those two equal shares. This transition makes the concept stick.
From Manipulatives to Masterpieces
The easiest way in is with a direct one-to-one connection. Right after a hands-on activity, gather your students and model how to draw what you all just created.
Keep your language consistent. Say things like, "We just folded our paper into four equal parts. Let's draw a rectangle on our whiteboards and show those same four parts." This repetition helps them see that the drawing is just a record of their action.
Fraction circles and bars are fantastic tools for this stage. Students can place the physical pieces on their desk and then draw them on paper right beside the manipulatives.
- Fraction Circles: These are perfect for representing parts of a whole like a pizza or a pie, linking directly to many of our food-based activities.
- Fraction Bars: These rectangular models are great for showing linear fractions and are a brilliant precursor to understanding fractions on a number line later on.
By having the physical object and the drawing side-by-side, students build a solid mental link between the two. The drawing becomes a symbol for the object, which is exactly the skill they need before moving to numerical symbols.
Creating Collaborative Anchor Charts
One of my favorite ways to document our learning is by making large, collaborative anchor charts. After a lesson on halves, we'll create a "Halves" chart together. Kids come up and contribute drawings of objects cut in half—a circle, a square, a sandwich—and we label everything together.
These charts become a living record of their discoveries. They serve as a visual reference point in the classroom that students can look to anytime they need a reminder. When a student is stuck, you can say, "Remember our anchor chart? What does a half look like?" It empowers them to find their own answers.
Teacher Tip: Don't strive for perfection on these charts. The goal is for them to be student-made. A slightly wobbly line drawn by a six-year-old that correctly shows two equal parts is far more valuable than a perfectly printed diagram. It shows their thinking.
Using Technology to Support Visual Learning
Let's be real—creating clear, consistent visual aids for every lesson takes time, and that's something teachers never have enough of. This is where a little help goes a long way. As you make this transition, understanding why animated video should be in your classroom can offer some great ideas for making abstract concepts like fractions more concrete on screen.
For creating your own printables, AI-powered tools are a total game-changer. An AI lesson planner like Kuraplan can generate kid-friendly diagrams, fraction models, and custom worksheets in minutes. You can ask it to create a page of circles for practicing halves or a set of rectangles for exploring fourths, perfectly aligning with your hands-on lesson. This ensures your visual aids are always clear and impactful, freeing you up to focus on the actual teaching.
These visual representations also provide an excellent foundation for more complex data visuals. You can explore this further by checking out our guide on the introduction to pie graphs.
Ultimately, moving from concrete to visual is about helping students organize their thinking on paper. By making this transition gradual, collaborative, and supported by great tools, we set them up for success when it's time to finally introduce formal fraction symbols.
Introducing Fraction Language and Symbols Naturally
After all that hands-on play with blocks, food, and drawings, your first graders have a really solid, gut-level feel for what a fraction is. Now it’s time to bridge that understanding to the formal math symbols. Think of it less as a huge leap and more like showing them the "official" way to write down what they already know.
The trick is to introduce the symbols as simple labels. When you hold up a card with 1/2 on it, you can say something like, "This is how mathematicians write 'one of two equal parts.' The bottom number, the denominator, tells us how many equal pieces we have in our whole. The top number, the numerator, tells us how many of those pieces we’re talking about right now."
This approach takes the mystery out of the notation. It’s not some scary, abstract code; it’s just a logical shorthand for an idea they've already figured out.
From Words to Symbols
To make this connection really stick, you’ll want to anchor it directly to the activities you’ve already been doing. Grab a paper plate you folded earlier and ask, "How many equal parts did we make?" When they say "two," write a 2 on the bottom. Then, point to one of the folded sections and ask, "And how many parts are we looking at?" When they say "one," write a 1 on top.
Do this over and over with different materials. The goal is to make building the fraction a shared, active process, not just some rule they have to memorize.
- Circle a group of objects: "Here are four counters. That's our whole group, so let's write a 4 on the bottom. Now, if I move one counter over here, how many am I talking about? One! So we write a 1 on top."
- Update your anchor charts: Go back to those collaborative charts you made and add the symbols 1/2 and 1/4 right next to the student drawings.
- Label everything: Have the kids practice writing the correct fraction symbol on their own drawings of divided shapes.
Tackling Common First-Grade Misconceptions
It’s almost a rite of passage for a first-grader to insist that 1/4 is bigger than 1/2. Why? Because 4 is bigger than 2! This isn't a sign that they're not getting it; it's a perfectly logical conclusion based on everything they know about whole numbers. Instead of just correcting them, let them discover the truth for themselves.
The best way to fix this is to go straight back to the hands-on stuff. Give them two identical pieces of paper. Have them fold one into halves and the other into fourths. Then, hold up one piece from each and ask, "Which piece is bigger?" That 'aha!' moment is something they will never forget.
This hands-on comparison proves that the more equal pieces you divide a whole into, the smaller each individual piece becomes. That tangible evidence is so much more powerful than just telling them the rule.
Global Perspectives on Early Fraction Learning
Interestingly, not everyone introduces fraction symbols at the same time. In some parts of the world, like Ontario, Canada, this is a core part of the grade 1 curriculum. The Ontario Math Curriculum actually mentions the word "fraction" 99 times starting in first grade, while "decimal" only appears 69 times, starting three years later. This shows a huge emphasis on building those foundational fraction concepts right from the start. You can discover more about the progression of fractions in curriculum standards.
For teachers looking to make this final step a little smoother, an AI tool like Kuraplan can be a real help. It can generate simple, clear worksheets that ask students to match the symbol (1/2) to the correct picture. It's the perfect kind of practice to solidify this final connection and turn their intuitive knowledge into formal mathematical understanding.
How To Assess and Differentiate Fraction Skills
After all the folding, cutting, and drawing, how do we really know if our students get it? When it comes to fractions for first grade, meaningful assessment rarely looks like a formal quiz. Instead, it’s all about sharp observation during the hands-on activities we’re already doing.
True understanding isn't about circling the right answer on a worksheet. It’s about hearing a student explain why their Play-Doh pizza is shared fairly. It's watching them confidently point to the "whole" before they even think about splitting it. These little moments are our most valuable data points.
Observation-Based Assessment and Simple Rubrics
Instead of a paper-and-pencil test, I rely on a simple checklist or rubric while students are working. This isn't anything fancy—just a clipboard with my students' names and a few key skills I'm looking for. It helps me see at a glance who needs a bit more guidance and who’s ready for the next step.
This is a classic example of formative assessment, which is perfect for guiding your day-to-day instruction. You can explore more ideas in these formative assessment examples.
A student’s ability to explain their thinking is the clearest window into their understanding. I’ll often ask, "How do you know those parts are equal?" or "Can you show me the whole shape again?" Their answer tells me more than any worksheet ever could.
Here’s a simple rubric that I’ve adapted over the years. It’s easy to use for quick check-ins.
| Skill | Emerging | Developing | Secure |
|---|---|---|---|
| Identifies the 'Whole' | Needs prompting to identify the whole object before partitioning. | Can identify the whole with occasional reminders. | Independently identifies the whole in various contexts. |
| Creates Equal Parts | Struggles to divide objects into equal shares without help. | Creates parts that are mostly equal; understands the concept. | Consistently and accurately divides objects into equal halves and fourths. |
| Uses Fraction Language | Rarely uses terms like 'half,' 'fourth,' or 'equal parts.' | Uses fraction vocabulary with some accuracy and prompting. | Uses terms like 'halves' and 'fourths' correctly and confidently. |
Differentiating Instruction For Every Learner
Every classroom is a mix of abilities, and our fraction lessons need to reflect that. The beauty of teaching fractions this way is that differentiation can be woven right into the activities you're already planning. We don't need three completely separate lesson plans; we just need a few smart modifications.
This table breaks down some quick, practical ways to differentiate your fraction activities on the fly.
Fraction Differentiation Strategies At-a-Glance
| Area of Focus | Support for Struggling Learners | On-Level Activities | Enrichment for Advanced Learners |
|---|---|---|---|
| Concrete Manipulatives | Provide pre-partitioned shapes with faint lines to guide cutting. Use self-correcting puzzles. | Students fold and cut their own shapes into halves and fourths using paper, Play-Doh, or food. | Challenge students to create thirds by folding a paper strip. This requires genuine problem-solving. |
| Conceptual Understanding | Focus on just one concept at a time, like identifying the "whole" or making "halves." | Students sort shapes into "equal parts" and "unequal parts" piles. | Ask students to explore non-examples, like drawing a circle that is not divided into fourths and explaining why. |
| Making Connections | Stick to tangible, real-world examples like sharing a cookie or a sandwich. | Students apply their knowledge to drawing tasks, like splitting a drawn pizza for two people. | Introduce composing new wholes with pattern blocks. Ask, "If two trapezoids make a hexagon, what fraction is one trapezoid?" |
These strategies ensure that every child can access the core concepts at their own pace, building confidence along the way.
This flowchart is a great little decision tree for figuring out when to introduce the abstract symbols for fractions.
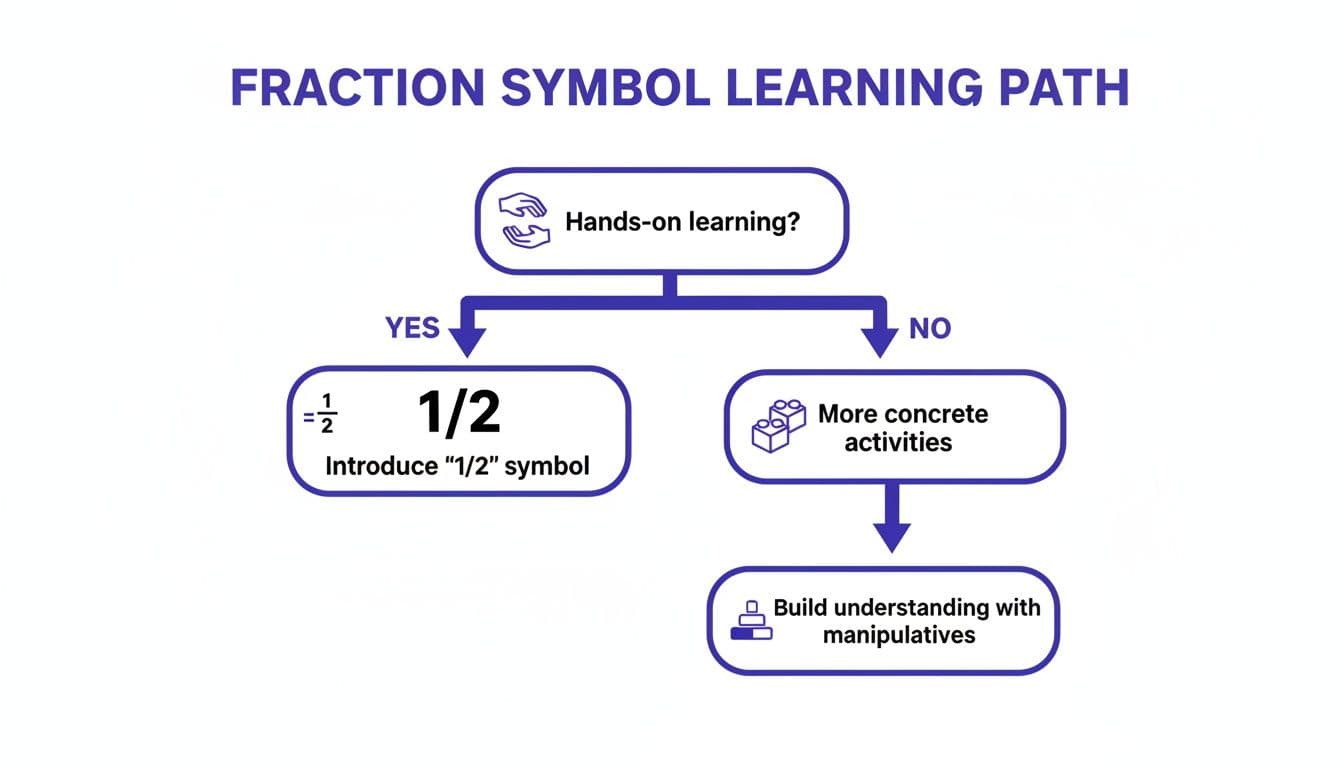
It’s a simple reminder: if a student is still working on the hands-on piece, they need more time with concrete materials before we push them toward the abstract symbols like 1/2 and 1/4.
Laying this strong foundation is critical. Research shows that while fraction content makes up just 3.2% of the first-grade math curriculum under Common Core, it skyrockets to 15.5% by fifth grade. Building a solid, differentiated foundation now is one of the most important things we can do for our students' long-term success in math.
Common Questions About Teaching First Grade Fractions
Even with the best lesson plans, teaching a new concept always brings up questions. Let's walk through some of the most common ones I've heard from other teachers (and asked myself!) when introducing fractions for first grade. These answers come straight from my own classroom experience and will hopefully help you feel more confident.
What Are the Most Important Fraction Concepts for a First Grader?
The goal here isn't to have first graders mastering complex operations. It’s all about building a deep, gut-level understanding of the absolute basics. You don't need to overwhelm them.
Just focus your energy on three key ideas:
- What a 'whole' is. This is the starting point for every single fraction conversation.
- The meaning of 'equal parts' or 'fair shares.' This is the heart and soul of first-grade fractions.
- Identifying and naming halves and fourths. These are the two foundational fractions they absolutely need to know.
If a student can confidently show you what one-half of a cookie looks like and explain why it's a half ("because it has two equal pieces!"), you've helped them build a fantastic foundation. It's so important to resist the urge to jump to written symbols until this hands-on understanding is rock-solid.
How Do I Address Students Thinking 1/4 Is Bigger Than 1/2?
Ah, the classic misconception! This is a perfectly logical conclusion for a first grader to make. Everything they know about numbers tells them that 4 is bigger than 2. Seeing this pop up is actually a good sign—it means they're trying to connect new information with what they already understand.
The best way to fix this is to go straight back to hands-on materials. Don't just tell them; let them prove it to themselves.
Give a student two identical pieces of construction paper. Ask them to fold one into halves and the other into fourths. Then, have them hold up one piece from each paper and ask, "Which piece is bigger?" That physical comparison is infinitely more powerful than any explanation you can give.
This tangible proof helps them build the crucial understanding that the more equal pieces you divide a whole into, the smaller each individual piece gets.
Are Worksheets an Effective Way to Teach Fractions?
Worksheets definitely have their place, but timing is everything. If you use them too early, you risk students just memorizing rules or coloring shapes without really getting the "why" behind it.
Worksheets are most effective after kids have had plenty of time for hands-on exploration. Think of them as a tool to record or reinforce what students have already learned with their hands and eyes. A good first-grade worksheet might ask a student to color one-fourth of a shape they just built with blocks or circle pictures that show equal parts. They should be a bridge from the physical to the abstract, not a replacement for it.
How Much Classroom Time Should This Unit Take?
A dedicated unit of one to two weeks is a great way to kick things off, but the real magic happens when you weave fraction language into your daily classroom routine all year long. That continuous, low-stakes reinforcement is what makes the ideas stick.
For example, you can talk about things like:
- Lining up in "two equal groups."
- Sharing art supplies into "four equal piles."
- Asking students to fold their paper in "half" before writing.
By integrating concepts like 'half' and 'whole' into everyday situations, you provide constant practice that cements their understanding long before and after the official unit is over.
Creating all these different materials—from hands-on activity guides to differentiated worksheets and visual aids—takes a ton of time. If you want to streamline your planning and make sure every student gets the support they need, a tool like Kuraplan can be a lifesaver. It helps you generate standards-aligned lessons, engaging activities, and custom visuals in minutes, giving you more time to focus on what you do best: teaching. Learn more at kuraplan.com.
